您现在的位置是:首页 > 电路图 > 电路图学习 > 电路图学习
电阻电路的等效变换详细解析
![]() 转载来源:电子技术应用-AET chinaaet.com 电子发烧友 elecfans.com2017-08-18
转载来源:电子技术应用-AET chinaaet.com 电子发烧友 elecfans.com2017-08-18
简介等效变换 等效是电路分析中一种很重要的思维方法。根据电路等效的概念,可将一个结构较复杂的电路变换成结构简单的电路,使电路的分析简化。 等效的概念 【二端电路(一端口电
等效变换
等效是电路分析中一种很重要的思维方法。根据电路等效的概念,可将一个结构较复杂的电路变换成结构简单的电路,使电路的分析简化。
等效的概念
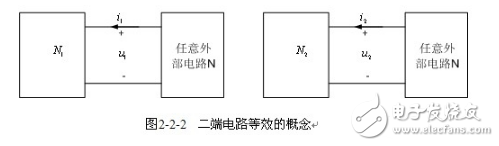
【二端电路(一端口电路)】 两端电路具有以下特点:只有两个端钮(a,b)与外部电路相连;进出端钮的电流相同,如图2-2-1所示。二端电路元件,例如电阻元件、独立源、电容元件、电感元件,可视为二端电路的特例,也称二端元件。二端电路也称为一端口电路,一端口电路端口电压、电流的关系称为一端口网络的端口特性或端口VCR。

【等效电路】 两个二端电路![]() ,
,![]() ,如图2-2-2所示,无论两者内部的结构如何不同,只要它们的端口电压、电流的关系( VCR)相同,则称
,如图2-2-2所示,无论两者内部的结构如何不同,只要它们的端口电压、电流的关系( VCR)相同,则称![]() 和
和![]() 是等效的。两个内部结构不同的电路等效的唯一标准是两者对应端口处的VCR完全一致,即它们对同一任意外部电路的效果完全相同。等效是对外部电路而言的,对于互相等效的两个电路
是等效的。两个内部结构不同的电路等效的唯一标准是两者对应端口处的VCR完全一致,即它们对同一任意外部电路的效果完全相同。等效是对外部电路而言的,对于互相等效的两个电路![]() ,
,![]() ,内部的工作状态是不等效的。等效具有传递性,如果二端电路
,内部的工作状态是不等效的。等效具有传递性,如果二端电路![]() 和
和![]() 等效,二端电路
等效,二端电路![]() 又与
又与![]() 等效,则必有
等效,则必有![]() 与
与![]() 等效。
等效。
电阻的串联与并联等效变换
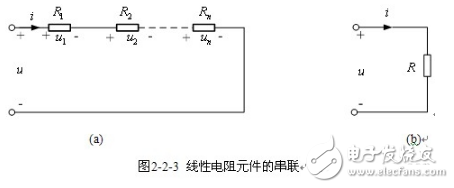
【电阻元件的串联】图2-2-3(a)中,由KVL得
![]()
且 ![]()
由KVL得 ![]()
令
![]()
则 ![]()
根据上式可以构造一个相应电路如图2-2-3(b)所示,所以图(a)和(b)是等效的,等效电阻等于各串联电阻元件电阻之和。
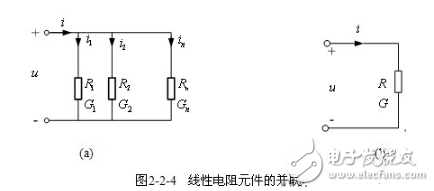
【电阻元件的并联】图2-2-4(a)中,由KCL得
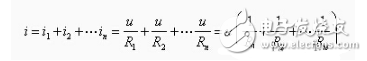
令 ![]()
用等效电导表示为
![]()
星形电阻网络与三角形电阻网络的等效变换
由线性电阻元件混联构成的网络,其最简等效电路为线性电阻。但是并非所有由线性电阻元件混联构成的网络都能通过串、并联化简为线性电阻。本小节介绍“平衡电桥”和“星形-三角形”互换两种化简方法。通过这两种方法,在结合电阻元件的串联、并联化简,可实现任何由线性电阻混联构成的网络的等效化简。
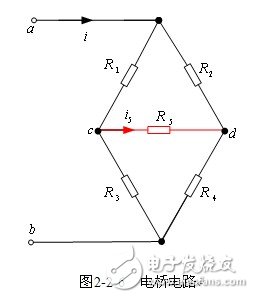
【平衡电桥】图2-2-6所示由5个线性电阻(为必要条件)构成的桥式电路中,当![]() 或
或![]() (由于
(由于![]() 为线性电阻,该两个条件必是同时成立的)时,称此桥式电路为平衡电桥。由平衡电桥电路特点可得到平衡电桥的两种等效电路。由
为线性电阻,该两个条件必是同时成立的)时,称此桥式电路为平衡电桥。由平衡电桥电路特点可得到平衡电桥的两种等效电路。由![]() 得到图2-2-6所示等效电路;由
得到图2-2-6所示等效电路;由![]() 得到图2-2-6所示等效电路。
得到图2-2-6所示等效电路。
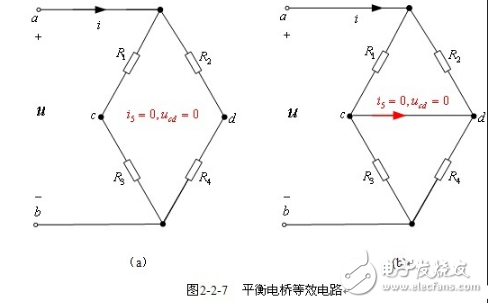
【电桥平衡条件】在图2-2-7(a)所示电路中,有
![]()
在电路2-2-7(b)中 ,有
![]()
由以上两式均可以推出电桥平衡的条件,为
![]()
【星形—三角形互换】 当电桥不满足平衡条件时,必须采用星形(Y形)与三角形(△形)互换才能将电桥电路化成线性电阻。
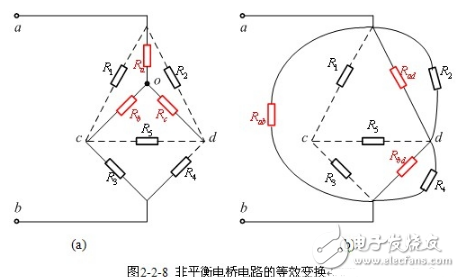
如果可将图2-2-6中以节电a,c,d为顶点的三角形电阻![]() ,
,![]() 和
和![]() 等效变换成图2-2-8(a)中以新节点o为中心的星形连接电阻
等效变换成图2-2-8(a)中以新节点o为中心的星形连接电阻![]() ,
,![]() 和
和![]() ;或者将图2-2-6中,以c为中心的Y形连接电阻
;或者将图2-2-6中,以c为中心的Y形连接电阻![]() ,
,![]() 和
和![]() 等效变换成图2-2-8(b)中以节点a,b,d为顶点的△形连接电阻
等效变换成图2-2-8(b)中以节点a,b,d为顶点的△形连接电阻![]() ,
,![]() 和
和![]() 。这样各电阻之间连接关系成为串联和并联关系了。也可以选择△cbd变成Y形,或选择以d为顶点的Y形变为△形。
。这样各电阻之间连接关系成为串联和并联关系了。也可以选择△cbd变成Y形,或选择以d为顶点的Y形变为△形。
【星形—三角形互换条件】根据前面等效的概念,分别求出这两种电路端钮处的电压-电流关系,让两者相同,即可获得等效条件。
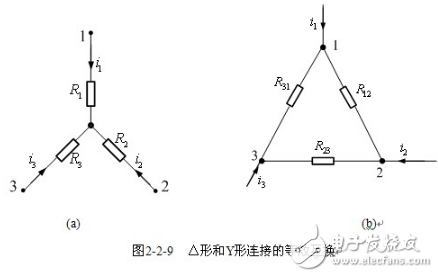
在△形电路中,有

求解得△形电路中的电压-电流关系

而Y形电路中的电压-电流关系为

两种电路等效,则端钮处的电压-电流关系应相同。比较△形电路和Y形电路的电压-电流关系,可得△形电路等效变换成Y形电路的条件为
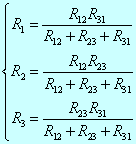 (△→Y)
(△→Y)
同理可得Y形电路等效变换成△形电路的条件为
 (Y→△)
(Y→△)
【例2-2-1】 求图2-2-10(a)所示电路的电流I。
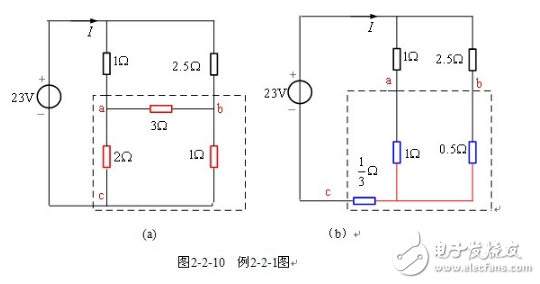
将图2-2-10(a)中![]() ,
,![]() ,
,![]() 所构成的三角形电路按
所构成的三角形电路按![]() 等效变换为(b)所示电路。则
等效变换为(b)所示电路。则
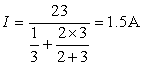
4、实际电源的两种模型及其等效变换
独立电源是可以用来描述实际电源的电路元件。以下讨论实际直流电源的电路模型。
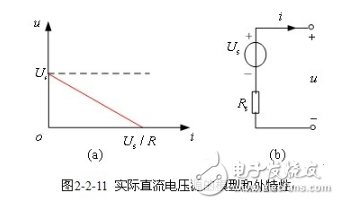
【实际直流电压源模型(戴维宁模型)】 一个实际直流电压源的端电压并不是恒定不变的,而是随着输出电流的增加而下降。实际直流电压源外部特性可用图2-2-11(a)所示曲线描述。根据曲线的形状可用独立电压源和线性电阻元件串联的模型来等效,图2-2-11(b)为该实际电源的电路模型,称为戴维宁模型。模型特性方程为
![]()
当实际电压源内阻![]() 很小时,特性曲线趋于与i轴平行,当
很小时,特性曲线趋于与i轴平行,当![]() 时,特性曲线与i轴平行,成为理想电压源。
时,特性曲线与i轴平行,成为理想电压源。
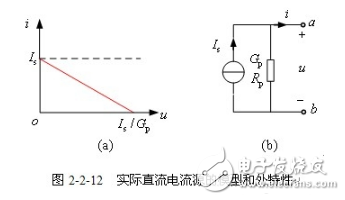
【实际直流电流源模型(诺顿模型)】 一个实际直流电流源,其电流并不是恒定不变的,而是随着端电压的增大而下降。实际直流电流源外部特性可用图2-2-12(a)所示曲线描述,并用图2-2-12(b)所示电路模型来等效,称为诺顿模型,电路模型的端口的特性方程为
![]()
当实际电流源内电导![]() 很小时,特性曲线趋于与u轴平行,当
很小时,特性曲线趋于与u轴平行,当![]() 时,实际电流源成为独立电流源。
时,实际电流源成为独立电流源。
【戴维宁模型和诺顿模型的互换】 图2-2-13(a)实际电压源端口电压-电流关系为
![]()
图2-2-13(b)实际电流源端口电压-电流关系为
![]()
欲使两种模型等效,则要求端口电压-电流关系相同,由此可得出元件参数应满足
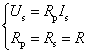
或者
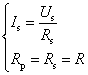
进行等效变换时应注意:
(1)电流源电流的参考方向由电压源的负极指向正极;
(2)等效是对外部电路而言的,对两电路内部的电阻之间、电压源和电流源之间是不等效的;
(3)等效变换条件也适用于受控电压源构成的戴维宁支路和受控电流源构成的诺顿支路,注意在电路变换中控制支路应保留。

5、电源等效转移
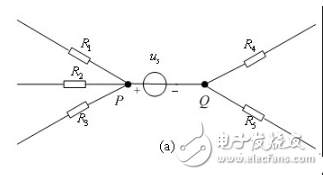
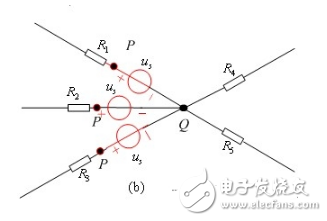
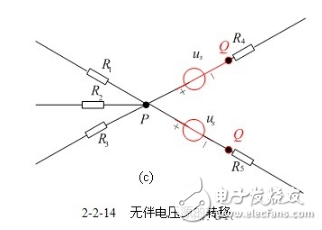
【无伴电压源转移】电压源没有与之串联的电阻而单独成为一条支路,称为无伴电压源支路,图2-2-14(a)所示无伴电压源可以进行以下等效变换。图2-2-14(b)是按P节点转移,图2-2-14(c)是按Q点转移。本质上是将电压源按照结点所连支路数裂开,注意图中结点的变化。
【无伴电流源转移】电流源没有与之并联的电阻而单独成为一条支路,称为无伴电流源支路。无伴电流源可进行以下等效变换。变换规则为:将电流源顺其原来的参考方向,转移到包含电流源的任意一个回路中的各支路上,并与这些支路并联,原无伴电流源所连接的两节点之间开路。