异步电机的动态数学模型坐标变换

    异步电机的动态数学模型十分复杂，不要说求解，仅要求画出很清晰的结构也并非易事。如果能将交流电机的物理模型等效地变换成类似直流电机的模式，分析和控制问题就可以大为简化。坐标系变换正是按照这条思路进行的。在这里，不同电机模型彼此等效的原则是在不同的坐标下所产生的磁动势完全一致。

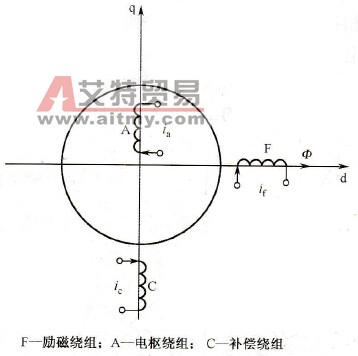
    图2-35    二极直流电机的物理模型

    众所周知，交流电机三相对称的静止绕组A、B、C，通过三相平衡的正弦电流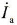、、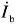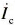时，所产生的合成磁动势是旋转磁动势F，它在空间呈正弦分布，以同步转速ω1（电流的角频率）顺着A-B-C的相序旋转。这样的物理模型如图2-36 (a)所示，它就是图2-34中的定子部分。产生同样的旋转磁动势F不一定非要三相，用图2-36 (b)所示的两个互相垂直的静止绕组α和β，通入两相对称电流同样可以产生相同的旋转磁动势F。可以认为图2-36 (b)所示的两相绕组与图2-36 (a)所示的三相绕组等效。

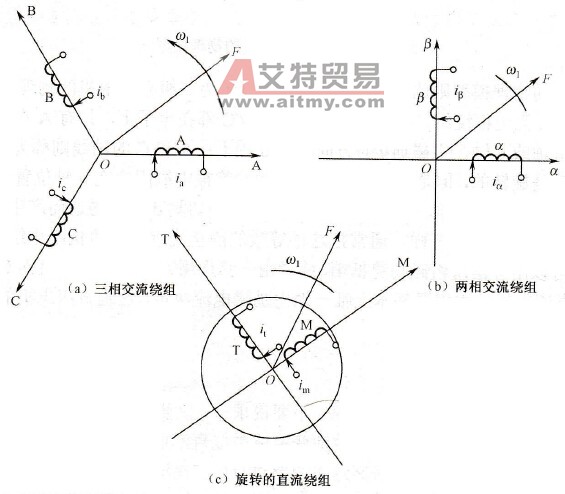
    图2-36    等效的交流电机绕组和直流电机绕组物理模型

    再看图2-36 (c)中的两个匝数相等且互相垂直的绕组M和T，其中分别通以直流电流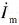和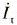，产生合成磁动势F，其位置相对于绕组来说是固定的。如果让包含两个绕组在内的整个铁芯以同步转速ω1旋转，则磁动势F自然也随之旋转起来，成为旋转磁动势。把这个旋转磁动势的大小和转速也控制成与图2-36 (a)和图2-36 (b)中所示的磁动势一样，那么这套旋转的直流绕组也就和前两套固定的交流绕组等效了。当观察者也站到铁芯上和绕组一起旋转时，在他看来，M和T是两个通以直流而相互垂直的静止绕组。如果控制磁通Φ的位置在M位置上，就和图2-35所示的直流电机物理模型没有本质上的区别了。这时，绕组M相当于励磁绕组，绕组T相当于伪静止的电枢绕组。

    这真是一种奇思妙想，一举突破了交流异步电机数学模型化简的难题。以产生同样的旋转磁动势为准则，图2-36 (a)所示的三相交流绕组，图2-36 (b)所示的两相交流绕组和图2-36 (c)中所示的整体旋转的直流绕组彼此等效。或者说，在三相坐标系下的ia、ib、ic，在两相坐标下的iα、iβ和在旋转两相坐标系下的直流磁动势im、it是等效的。它们能产生相同的旋转磁动势。就图2-36 (c)中的M、T两个绕组而言，当观察者站在地面看上去，它们是与三相交流绕组等效的旋转直流绕组；如果跳到旋转着的铁芯上看，它们就的的确确是一个直流电机的物理模型了。这样，通过坐标系的变换，可以找到与交流三相绕组等效的直流电机模型。至于如何解出ia、ib、ic与iα、iβ和im、it之间准确的等效关系，那是纯数学问题，是坐标变换的任务，解决的难度也减轻了许多。