拖动系统的运行状态是怎样决定的

    1．拖动系统的转矩平衡。电动机在带动负载运行时，其转速大小必符合如下规律：

   TM>TL→n↑

   T<TL→n↓

   TM=TL→n=const

式中  TM -电动机的转矩，N·m；

   TL -负载转矩（包括损耗转矩），N·m；

    n-系统转速，r/min。

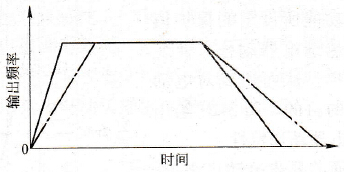
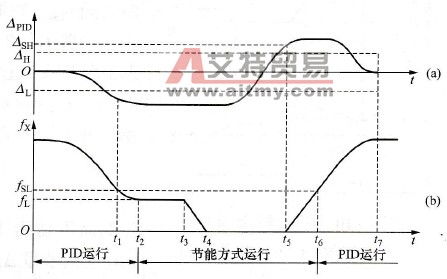
    2．拖动系统的工作点。拖动系统的运行状态由电动机机械特性和负载机械特性的交点决定，如图3-3中之Q点。图中，曲线①是电动机的机械特性，曲线②是负载的机械特性，Q点称为拖动系统的工作点，设Q点的转速为nQ，则：

   (1)转速下降为n1。当转速为n1时，电动机的转矩将增加为TM1，而负载的转矩将减小为TL1，显然：

   TM1>TL1，系统必将加速，随着转速的上升，TM逐渐减小，而TL逐渐增大，直至到了Q点，才能稳定下来，如图a）所示。

   (2)转速上升为n2。当转速为n2时，电动机的转矩将减小为TM2，而负载的转矩将增大为TL2，显然：

   TM2<TL2，系统必将减速，随着转速的下降，TM逐渐增大，而TL逐渐减小，直至到了Q点，才能稳定下来。

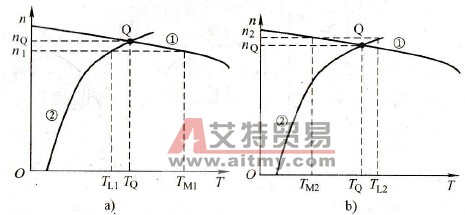
    图3-3    拖动系统的工作点

   a)转速低于工作点的情形b）转速高于工作点的情形

    所以，拖动系统只能在Q点稳定运行。

    3．拖动系统的习惯性分析。如上述，在稳定状态下运行时，电动机的转矩总是和负载转矩相平衡的。所以，习惯上在分析电动机的机械特性时，横坐标常常直接作为负载转矩来看待，如图3-4所示，通常的说法是：当负载转矩从TL1增加到TL2时，系统的转速将从n1下降为n2。

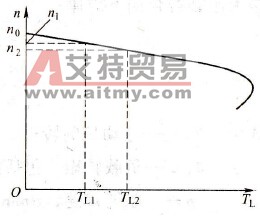
    图3-4    机械特性的习惯分析