异步电动机的动态数学模型

    1．坐标变换  异步电动机的定子绕组通常为三相绕组，转子为三相或多相绕组，没有励磁绕组，定子绕组磁动势和转子绕组磁动势共同作用产生异步电机的气隙磁场。为了减小定子电流的励磁电流分量，异步电动机的气隙长度较短。通过绕组的分布、短距、转子斜槽等措施，常用三相异步电动机的气隙磁场。在分析异步电动机动态过程时，为了便于在工程应用中的分析，有必要对异步电动机的模型加以“理想化”。“理想化”的异步电动机有如下的假定。

   a)忽略电动机铁心的饱和、磁滞及涡流的影响，铁心及导线的趋表效应也不考虑。

   b)忽略定子、转子谐波磁动势的影响，即认为气隙磁势按正弦分布。

   c)忽略定子、转子齿槽影响，即认为气隙是均匀的。

   d)转子为三相绕组。

    根据这些假设，“理想化”异步电动机定子绕组的自感系数L1、转子绕组的自感系数L2、定子三相绕组之间的互感系数MUV、MVω、MWU，以及转子多相绕组之间的互感系数均为常数。而定、转子绕组之间的互感系数Msr为

   Msr=Mcosγ    (7-7)

式中γ-定子u相绕组中心线与转子u相绕组中心线之间的电角度为

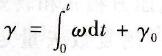    (7-8)

式中  γ0-转子位置初始位置角；

    ω-转子电角速度。

    当γ=0时，即定、转子绕组的中心线重合时它们之间的互感为最大。当转子旋转时，定、转子绕组之间的互感系数Msr是时变系数。

    可以用异步电动机的自感系数、互感系数等参数，选择电动机的定、转子电流（或磁通）作为状态变量，写出电动机的状态方程式。假定三相电动机没有中性线，那么定子三相电流是相关的（三相电流之和为0），因此描述三相交流电动机定子电流的独立变量只有2个。同理，在将转子绕组等效为三相绕组以后，描述转子电流的独立变量亦为2个。这样一来，三相异步电动机的状态方程式为4阶微分方程组（假定电动机的速度为常数）。如果考虑电动机的运动方程式，那么三相异步电动机的状态方程式为5阶微分方程组。但是这样写出的数学模型是个有时变参数的非线性微分方程组，分析较为困难。

    根据电动机过渡过程的理论，可以通过坐标变换使问题简化。它的基本思路是将三相异步电动机等效为空间上互差90°的两相电动机，由此推导出电动机的状态方程式。这种数学模型的阶次不变，仍为5（或4）阶。这种变换从物理意义上不难理解。因为电动机的机电过程是通过磁场而作用的，只要变换前后的磁场不发生变化，电动机的机电过程就不会发生变化。事实上，在学习电机理论时，三相交流电动机能以三相对称电流可以产生圆型旋转磁场，两相电动机通以两相对称电流亦可以产生圆型旋转磁场。换个角度考虑，从产生圆型旋转磁场出发，不必去追究这个磁场是两相绕组产生的，还是三相绕组产生的。从数学角度考虑，任何一个状态空间均可经过线性变换，变换到另一个线性空间。状态方程组在进行线性变换时，其维数不发生变化，且为一一对应的。

    2．d-q坐标系上的电压方程式和转矩方程  在d-q坐标系上电动机的电压方程式可以用复数矢量定子电压u2dq、定子电流i1dq、转子电流i2dq为

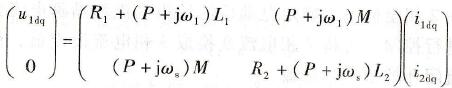    (7-9)

    如果使用转子磁链ψ2dq

   ψ2dq=Mi1dq+L2i2dq    (7-10)

    则电压方程式变为

    (7-11)

    电磁转矩计算公式为

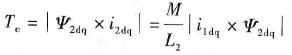    (7-12)

    式中  ω1-同步电角速度；

    ω2-转子转差角频率。