石英挠性加速度计数字闭环检测电路噪声研究

　　张声艳，刘冬，冯忠伟，陈玉坤

　　（中国运载火箭技术研究院 研究发展中心，北京 100076）

       摘要：为解决目前数字闭环石英挠性加速度计（Digital ClosedLoop quartz flex Accelerometer, DCLA）实测精度与其理论极限精度存在一个数量级的问题，进行DCLA闭环检测电路噪声分析。建立闭环系统误差模型，采用噪声逐级检测的方法，搭建基于噪声分离的开环噪声测试平台，确定差动电容检测环节（C/V）是影响系统精度的主要因素。在此基础上，对改进后的试验样机开展零偏稳定性测试，并对试验结果进行Allan方差分析。实验结果表明，改进后的DCLA系统精度由65.49 μg提高到12.24 μg，与理论精度基本一致，充分验证了理论分析方法的正确性，为进一步改善和优化数字闭环加速度计系统提供指导和依据。

　　关键词：数字闭环;石英加速度计;检测电路;噪声分析

0引言

　　石英挠性加速度计具有精度高、长期稳定性好、体积小、结构简单等优点，在各种惯性导航、制导、测量和控制领域发挥着重要作用［12］。传统石英挠性加速度计一般采用模拟伺服电路，输出为模拟信号，需外加开环模数转换电路才能为导航计算机提供数字信息，而转换过程中将不可避免地造成精度损失，并随时间累积。目前，国内学者对石英挠性加速度计的研究主要集中在表头组件及模数转换电路（I/F、V/F、A/D）的改进上。尽管I/F与V/F方案能够达到较高的转换精度，但由于采用测频芯片，决定了系统的转换速率不可能很快，且成本较高；对于A/D转换方案，系统转换精度受限于芯片位数，尤其是在小信号情况下，系统转换误差较大［3］。可见，模拟式石英挠性加速度计对所用器件的依赖性大，难以解决精度损失的问题。

　　本文提出的基于数字闭环方案的石英挠性加速度计，可直接输出数字量，理论上不存在开环模数转换带来的精度损失，且由于采用模拟电流反馈的方式，可避免因脉冲加剧引起的表头疲劳问题［4］，具有抗干扰能力强、可靠性高、可控性强等优点，具有广泛的应用前景。

　　随着高精度惯导系统的不断发展，对加速度计的精度要求也越来越高，而噪声是制约数字加速度计系统精度的重要因素，因此为提高数字加速度计的测量精度，需要对系统噪声特性进行深入研究。本文基于现有石英挠性摆式加速度计数字闭环检测方案，根据误差的产生机理确定闭环系统中存在的各误差源，建立闭环系统误差模型，分析了各误差参数对系统精度的影响，最后通过噪声分级测试，确定影响系统精度的关键环节，并在此基础上对实验样机进行改进及测试，从而验证理论分析结果。

1工作原理

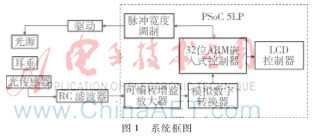
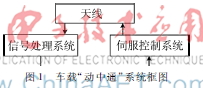
　　本文所研究的数字式加速度计检测系统框图如图1所示，主要由机械表头和数字闭环检测电路两大部分组成。表头检测质量组件由镀膜石英摆片和粘接在它上面的两个力矩器线圈组成，通过挠性摆片和上、下极板组成的差动电容将敏感到的外界加速度转换为可检测的电信号传送到数字闭环检测电路作进一步处理［5-6］。

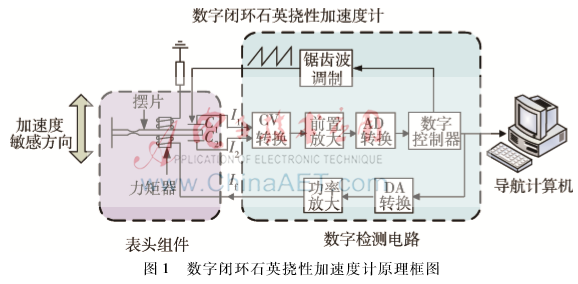
       数字闭环检测电路以FPGA为核心，主要包括电容调制信号、模拟差分放大、数字信号处理和反馈电流驱动四部分，代替了传统的模拟检测电路和后续的模数转换环图3噪声在闭环系统中传递仿真模型节，其主要功能包括：(1)产生用于调制加速度计表头电容的调制信号；(2)接收由表头输出的加速度信号；(3)输出与加速度信号成线性关系的反馈电流信号，以实现伺服平衡；(4)直接输出数字信息给导航计算机。

2理论研究

　　2.1误差模型建立

　　根据DCLA系统信号流向，建立闭环系统误差模型，如图2所示。其中ain为沿输入轴作用的加速度，ap为沿摆轴作用的加速度，KB为摆性，Md为干扰力矩，J为摆组件绕输出轴的转动惯量，C为摆组件的阻尼系数，Ks为挠性摆组合刚度，β为信号传感器机电零位与摆组件机械零位之间的弹性恢复角，k1为差动传感器系数，kCV为C/V转换电路伺服放大器增益系数，kAD为A/D转换系数，kDA为D/A转换系数，kVI为V/I转换环节的转换系数，kt为力矩器系数，nCV为电路热噪声，nAD为A/D量化噪声，nDA为D/A量化噪声。

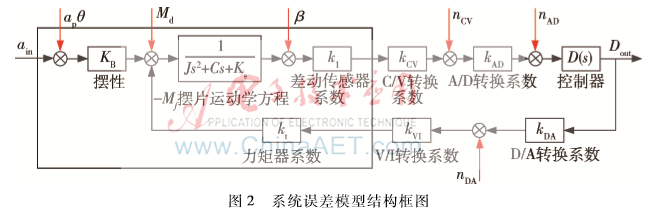
       可以看出，本系统中主要存在的噪声环节有表头组件环节、差动电容检测环节、A/D转换环节及D/A转换环节，通过理论分析，得出各环节噪声均方根值如表1所示［7］。在数字加速度计系统输出端污染噪声为白噪声的情况下，可得到闭环检测系统1 s输出时的理论精度为5.236 4 μg。

　　2.2Simulink建模仿真

　　基于上述分析结果，在连续域及数字域分别建立基于各环节噪声源的Simulink仿真模型，如图3所示。

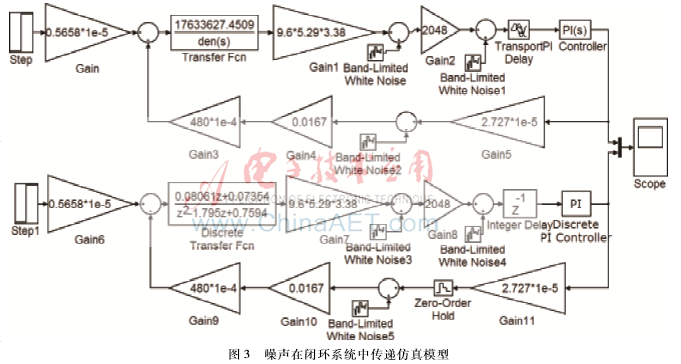
　　根据仿真结果，可以看出差动电容检测环节是影响系统精度的主要因素，其噪声水平与A/D、D/A转换器位数无关，因此为提高系统静态精度水平，需进一步改善电容检测环节的性能。

3实验研究

　　3.1开环噪声分级测试

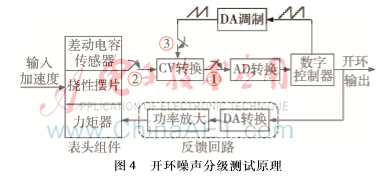
　　为分析数字加速度计检测电路前向通道中各噪声源对系统输出的影响，在开环情况下，采用由后至前、逐级检测的方法进行噪声分级测试［8］，实验原理如图4所示。

　　首先，断开反馈及调制通道并将A/D输入端接地，所得加速度计的开环输出为A/D环节的量化噪声；其次，恢复C/V转换与A/D转换之间的连接，并将差动电容输入端接地，所得输出为C/V及A/D两个环节的综合噪声；最后，接通调制环节并将两

　　个电容值相等的独石电容代替表头电容，所得输出为调制、C/V及A/D三个环节的综合噪声。

　　根据噪声独立作用原理，利用方和根公式，计算得到A/D量化噪声、C/V检测电路噪声、调制环节噪声等效加速度分别为0.709 μg、18.918 μg、3.423 μg。可以看出，开环情况下，A/D量化噪声对系统精度影响较小，而C/V检测电路噪声所占比例为82.07%，其对系统精度的影响是最为显著的。

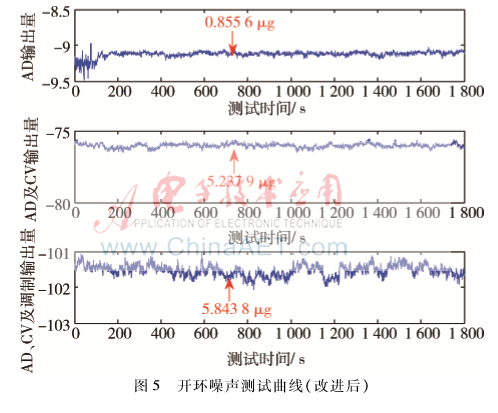
　　上述理论及试验结果均表明差动电容检测电路是影响系统精度的主要因素，因此对其进行如下改进：（1）采用T型电阻网络配置的方法，解决了大阻值与低噪声之间的矛盾；（2）采用“驱动电缆”及等电势屏蔽技术以减小表头寄生杂散电容影响。对改进后的样机重复进行上述开环噪声测试实验，测试结果如图5所示，测得A/D量化噪声、C/V检测电路噪声、调制环节噪声等效加速度分别为0.856 μg、5.168 μg、2.591 μg。可以看出，改进后样机噪声水平有了较大的改善。

　　3.2零偏稳定性试验

　　在稳态情况下，数字加速度计的静态输出是一个平稳随机过程，其输出值将围绕均值起伏波动，零偏稳定性作为衡量加速度计静态精度性能的重要指标，可以采用功率谱噪声密度PSD、阿伦方差或均方根有效值进行评价。本文基于改进后的样机，搭建DCLA系统测试平台，如图6所示，在该平台下开展DCLA零偏稳定性试验，同时类比于光纤陀螺数据分析方法，采用Allan方差方法对改进后的DCLA系统精度进行评价。

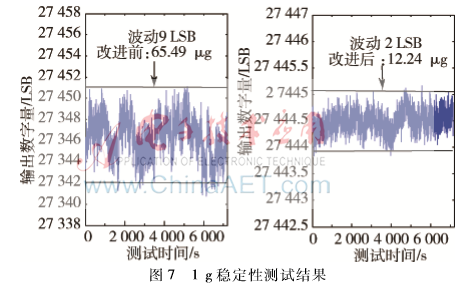
　　图7所示为数字加速度计改进前后，在1 g位置下输出稳定性测试结果。根据所得数据计算标准偏差，改进后系统精度（零偏稳定性）由65.49 μg提高到12.24 μg，与理论精度仍存在一定差距，其原因在于系统输出信号并非理想的白噪声分布，因此实测精度低于N法则下的理论精度。

　　3.3Allan方差分析

　　本实验中静态采集加速度计1 h输出数据，将采样时间间隔设置为10 ms，类比光纤陀螺得出加速度计中各项噪声［9］，得出加速度计Allan标准差双对数曲线如图8所示。

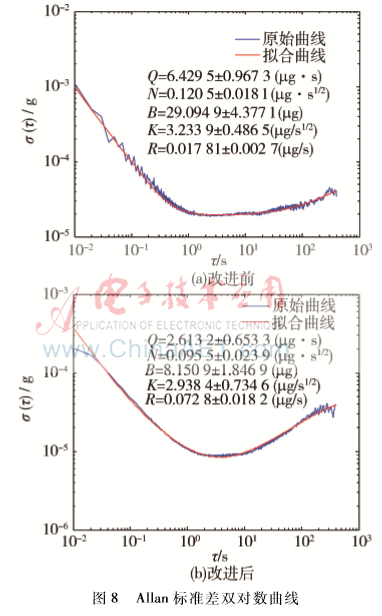
　　可以看出，改进后样机Allan标准差双对数曲线较为平滑，除加速度斜坡系数R外，量化噪声系数Q、速度随机游走N、零偏不稳定性系数B、加速度随机游走系数K的指标均有较大改善。

4结束语

　　本文根据数字闭环加速度计的工作原理，通过对表头机械环节、差动电容检测电路环节以及A/D、D/A转换环节的噪声特性进行深入分析，并通过噪声分级测试，验证了差动电容检测电路是影响系统精度的主要环节，对改进前后的系统样机进行零偏稳定性测试，系统精度由65.49 μg提高到12.24 μg，实测结果与理论精度基本处于同一量级，同时引入Allan方差对改进后样机进行性能评价，能够满足高精度惯性导航系统的使用要求。

　　本文研究成果可为优化和改善数字闭环加速度计系统的测量精度提供理论依据和实践指导，且相关研究方法也可用于其他微弱信号检测系统的精度分析。

　　参考文献

　　［1］ 顾英.惯性加速度计技术综述［J］.飞航导弹,2001,18(6):78-85.

　　［2］ 王巍.高精度加速度计测量系统的分析与设计［D］.哈尔滨:哈尔滨工程大学,2011.

　　［3］ 魏渊.数字闭环石英挠性加速度计系统设计与实现［D］.北京:北京航空航天大学,2012.

　　［4］ 易洪雯.石英挠性加速度计二元调宽数字脉冲控制系统的研制［J］.中国惯性技术学报，1996,4(4):31-36.

　　［5］ 张晞,张声艳,曹巧媛.数字闭环石英挠性加速度计量化误差分析及实验研究［J］.传感器与微系统， 2013.32(11):33-36.

　　［6］ 张晞,张声艳,李立京,等.环路参数对数字闭环加速度计动态特性影响［J］.北京航空航天大学学报，2014,40(4):455-460.

　　［7］ 张晞，张声艳.数字闭环石英挠性加速度计信号检测技术［J］.红外与激光工程，2014,43(10):3356-3362.

　　［8］ 冯丽爽,粟妮,雷明，等.谐振式集成光学陀螺噪声分析与实验研究［J］.光学技术,2012(6):712-717.

　　［9］ 严恭敏.惯性仪器测试与数据分析［M］.北京：国防工业出版社,2012.