采用了变频器后功率因数究竟是高还是低

    变频器输入侧的功率因数是较低的，但并不是由于cosφ的原因。说明如下：

    1．变频器输入电流波形如前述，“交-直-交、电压型”变频器的输入侧是整流和滤波电路。显然，只有当电源线电压的瞬时值uL大于电容器两端的直流电压UD时，整流桥中才有充电电流。因此，充电电流总是出现在电源电压的振幅值附近，呈不连续的脉冲形状，如图1-29a、b和c所示。它具有很强的高次谐波成分。有关资料表明，输入电流中的5次谐波和7次谐波分量是很大的，其谐波分析如图1-26d所示。

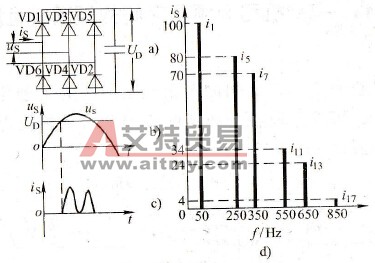
    图1-29    输入电流的波形及其谐波分析

   a)电路  b）电压波c）电流波d）谐波分析

    2．功率因数的定义与分析

   (1)功率因数的定义。电路所消耗的平均功率和视在功率之比称为功率因数：

   λ=P/S    (1-17)

式中  λ=功率因数；

   P-平均功率，kW；

   S-视在功率，kVA。

    功率因数小于1的根本原因，是出现了无功功率的缘故。

   (2)电流与电压频率相同时的平均功率。当电流和电压的频率相同时，功率因数的大小取决于电流与电压之间的相位关系。

    如图1-30a，假设电流比电压滞后φ角：

   φ=2πft=ωt    (1-18)

式中  φ-功率因数角，即电流比电压滞后的电角度；

   f-电流的频率，Hz；

   t-时间，s；

    ω-角频率。

    功率的瞬时值p等于电压u和电流i瞬时值的乘积：

   p=ui    (1-19)

由图知：

    在0~t1段：u为“+”，i为“-”。所以，p为“-”值；

    在t1~t2段：u和i都为“+”。所以，p为“+”值。

    下半周也一样。

    可见，平均功率被滞后时段内的负功率抵消掉一部分。正、负抵消的功率称为无功功率。滞后角越大，无功功率也越大，平均功率越小。

    滞后角的余弦cosφ称为位移因数。

   (3)高次谐波电流的平均功率。以5次谐波电流为例，它所消耗的功率瞬时值的大小等于5次谐波电流瞬时值和电压瞬时值的乘积：

   p5=ui5

式中  p5-5次谐波电流的功率瞬时值，kW；

   i5-5次谐波电流的瞬时值，A。

    由上式算得的功率曲线如图1-30b所示。由图知，瞬时功率的一部分为“+”，另一部分为“-”。可以证明，在一个周期内，正功率的总和与负功率的总和正好相等，平均功率等于0。

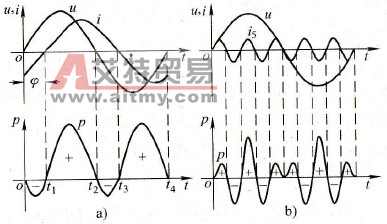
    图1-30    电路消耗的瞬时功率

   a)电流滞后的特点b）谐波电流的特点

    所以，所有高次谐波电流的平均功率都等于0，都是无功功率。

    非正弦电流中，高次谐波电流所占的比例，称为畸变因数，等于电流基波分量的有效值与总有效值之比：

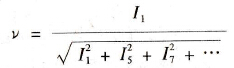    (1-20)

式中    v-畸变因数；

   I1-电流基波分量的有效值，A；

   I5、I7、…-分别是5次谐波电流、7次谐波电流、…的有

    效值，A。

   (4)完整的功率因数定义

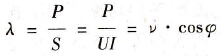   (2-21)

式中  λ-功率因数；

   cosφ-位移因数。

    3．变频器输入侧的功率因数  变频器中，输入电流的基波分量基本上与电压同相，故cosφ≈1；但电流的畸变因数较低。所以，变频调速系统的功率因数较低，约为0.7~0.75。

    因此，用功率因数表来测量变频器输入侧的功率因数是不正确的。因为，功率因数表是根据电动式偶衡表的原理制作的，其偏转角与同频率电压和电流间的相位差有关。但对于高次谐波电流，则由于它在一个周期内所产生的电磁力将互相抵消，对指针的偏转角不起作用。所以，功率因数表的读数将反映不了畸变因数的问题。